A Tutorial on Finite Difference Shock Capturing Schemes

CODE REPOSITORY LINK

This project focuses on the implementation of finite difference shock capturing schemes for the 1D Euler equations. The associated repository, containing tutorials on a variety of WENO schemes and the Roe scheme, can be found at the link above or in the repositories page.

WHAT THE REPOSITORY CONTAINS

This is a suite of codes for solving the 1D Euler equations. For those unfamiliar, these equations govern the flow of a frictionless gas in one dimension. The key feature of the 1D Euler equations is they allow for shock wave formation owing to their inherent non-linear nature, making them a simple set of equations that still captures some of the key physics that occurs during processes like supersonic flight, atmospheric re-entry, and stellar supernovae. In order to study the behavior of shock waves in a variety of situations, scientists and engineers often turn to numerical solutions of the Euler equations. However, properly simulating shock waves is a difficult task, particularly if one is interested in obtaining physically correct solutions with high orders of accuracy. The critical difficulty lies in obtaining a proper numerical approximation for the flux difference occuring across the shock wave discontinuity, which if not done properly can result in unphsyical solution oscillations (Gibbs phenomena), incorrect shock propagation speeds (convergence to the wrong weak solution), and numerical instability (unbounded growth of solution energy). This repository contains several finite difference based numerical methods that accomplish the task of properly capturing shock waves to various degrees. Several options for the spatial flux differencing scheme, time integration methods, and model problems for testing the numerical schemes are included.

SPATIAL FLUX SCHEMES

• First order Roe scheme

• WENO5 schemes as proposed by Prof. Chi Wang Shu and his collaborators
  • WENO5 Component wise reconstruction scheme
  • WENO5 Characteristic wise reconstruction - Lax-Friedrichs flux splitting approach
  • WENO5 Characteristic wise reconstruction - Roe flux splitting approach
• WENO6 schemes proposed by Hu and Adams
  • WENO6 Characteristic wise reconstruction - Lax-Friedrichs flux splitting approach
  • WENO6 Characteristic wise reconstruction - Roe flux splitting approach

TIME INTEGRATION SCHEMES

• First order explicit Euler method

• Third-order TVD Runge-Kutta method (“SSP-RK3”) of Shu and Osher

1D TEST PROBLEMS

• Sod’s shock tube problem

• Shu-Osher entropy wave/shock interaction

• A steady shock wave

• The Lax problem

• The 123 problem

SOLUTION VISUALIZATION AND COMPARISION

• Built in plotting routines for 1D profiles

• Ability to view x-t plane to visualze characteristic wave fronts

• Exact solutions (computed on fine meshes w/ high order schemes) for the following problems

  • Sod problem
  • Shu-Osher problem

WHAT THE REPOSITORY IS FOR

This repository started out as a project for a class I took on numerical methods for hyperbolic conservation laws, in order to help me better understand concepts like the Roe scheme, WENO schemes, and the more general principles of turning the theory of hyperbolic PDE solution techniques into actual working code. As such, the code in this repository is designed to be educational, and is written with copious comments that describe the methods being used and the papers and textbooks that are useful in understanding them. This might be especially useful for the new graduate student, scientist, or engineer who has not been directly exposed to the concepts of hyperbolic PDE theory, applied math, or computational gas dynamics before and is keen on learning how to implement them.

The code is also written in a highly modular fashion, with arguably more subroutines than necessary. This was done intentionally in the hopes of partitioning the code into digestable chunks that corresponde to a single step in the solution process (i.e, initial condition creation, flux reconstruction, time marching, plotting, etc.) and also to make the overall code easier to interact with.

I also want to stress that since the routines were written with education and user-friendliness in mind, they are not optimized for performance. For 1D problems, this really does not matter but if one wants to extend these concepts to effective 2D or 3D solvers, code optimization would be required.

HOW TO INTERACT WITH THE CODE

The entirety of the code is controlled by the routine ‘DRIVERSCRIPT.m’. Within this routine are the options to change the flux scheme, the time integration scheme, the test problem, and the visualization approaches. Comments are contained within this script that actually detail how to accomplish each of these tasks. Furthermore, each subroutine that the code calls contains comments that describe its purpose and document the mathematical steps occurring in each numerical algorithm. References to useful papers and textbooks are included where appropriate for the user to find more detail when desired. While the published code is written in Matlab, hopefully conversion to a different language can be accomplished in a relatively straightforward manner through the use of some online GPT.

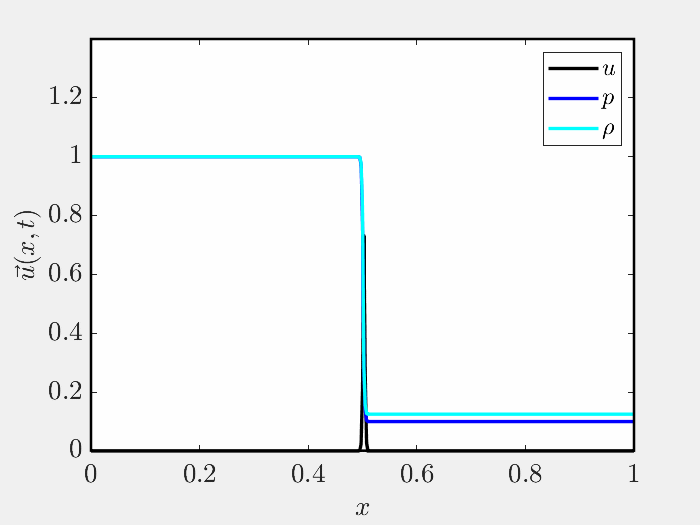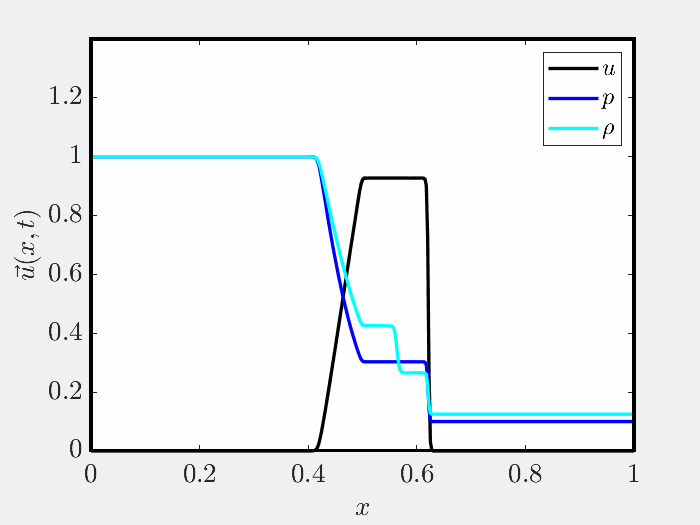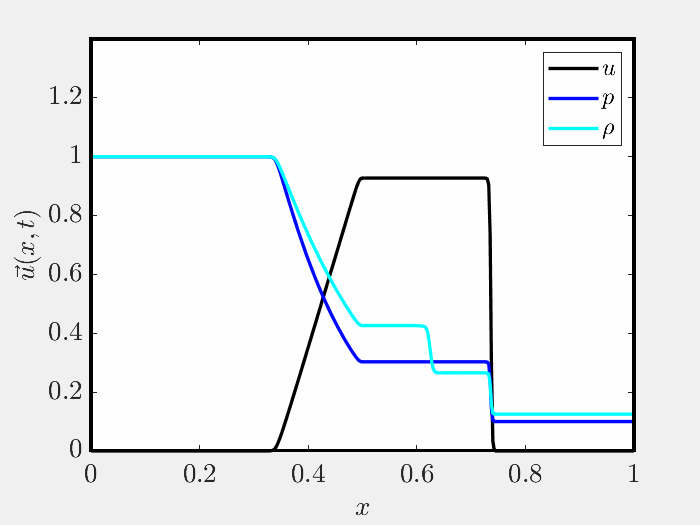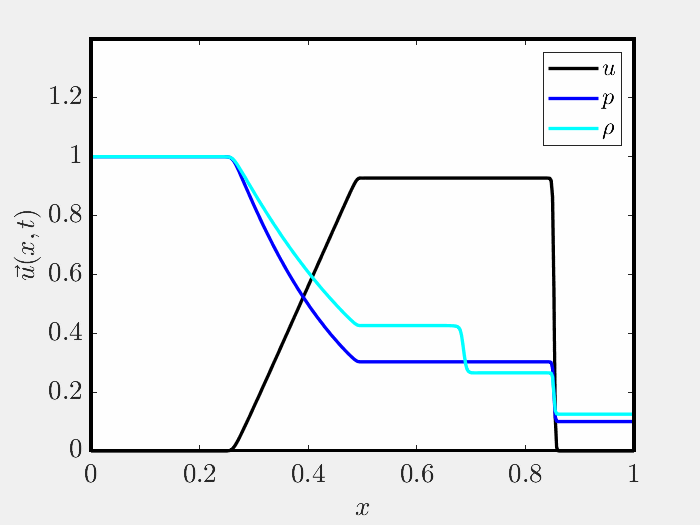
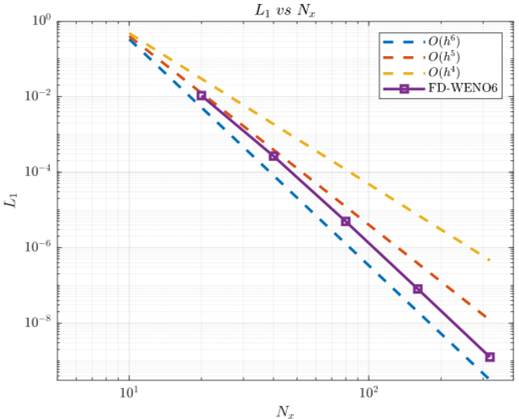
A HANDFUL OF FIGURES

Herein I’ve included several figures that demonstrate the validity of the code. Further figures may be found in the repository README.