Non-Stationary Analysis of Scramjet Unstart
Data driven analysis of the scramjet unstart problem using novel modal decomposition tools
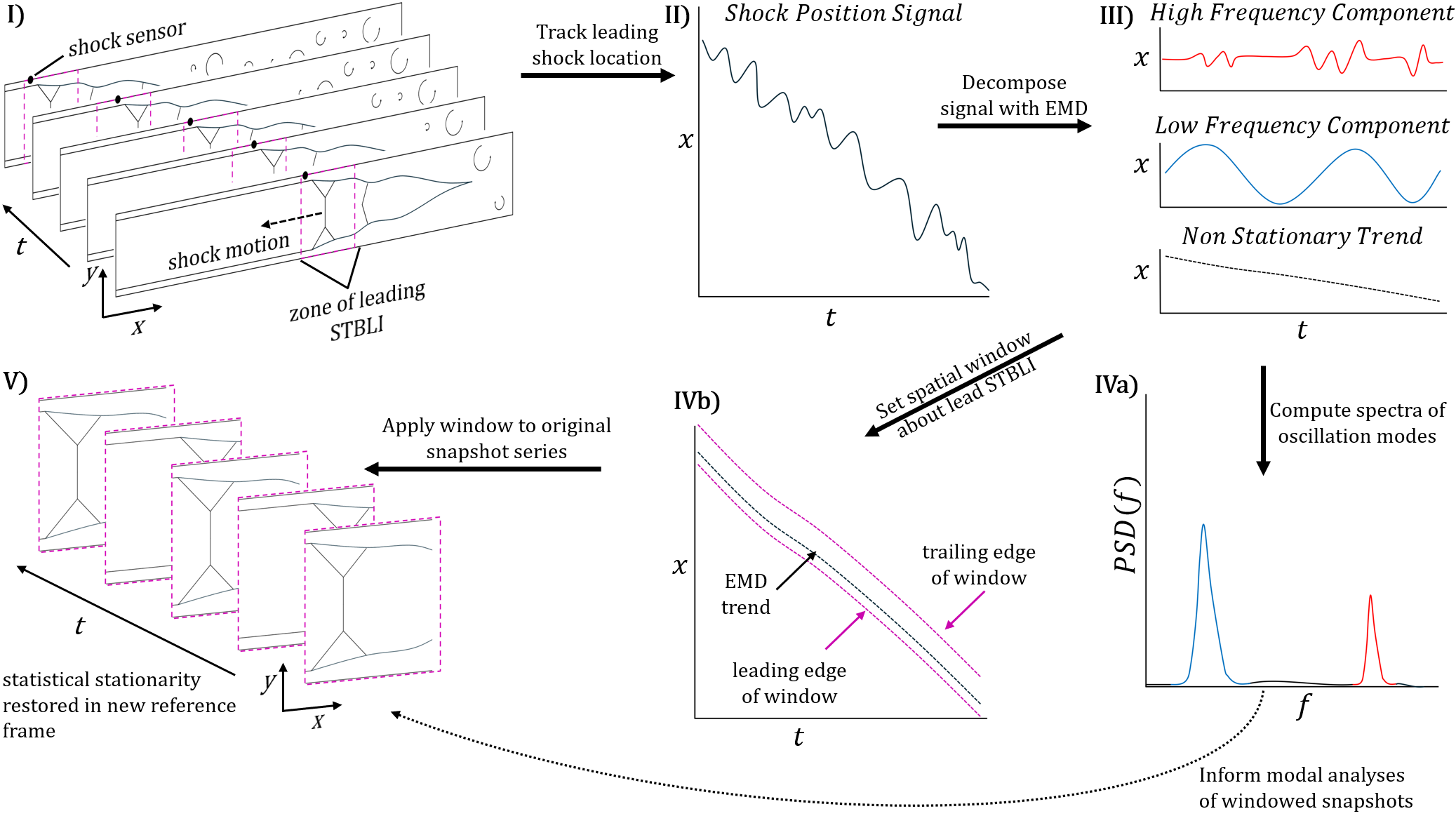
In this work, a novel analysis method for non-stationary flows is presented. The method is specifically designed to remove translation invariances from a given problem. Translational invariances occur frequently in wave propagation problems, where wavefronts propagate in various directions in a non-periodic manner. These invariances hinder the ability of common model order reduction techniques, especially data-driven ones. The proposed method removes these invariances, and does so in an entirely data-driven fashion. Furthermore, by removing the translational motion from the system, statistial stationarity is restored and analysis techniques like Proper Orthogonal Decomposition and Dynamic Mode Decomposition can be used. The process is demonstrated on an upstream propagating shock train, which mimics the dynamics associated with the hazardous problem of scramjet unstart. A manuscript detailing the method and its findings can be found on my ResearchGate page.